2. Using Inference Rules to Produce Predicate Calculus Expressions
- Inference Rules
기존에 주어진 추론을 통해 주어진 명제의 true,false를 가리는 것을, Inference Rule 이라고 한다. 아래의 예제를 보자
"Maxim will die" 라는 문장을 아래의 주어진 statement 들로 부터 증명하라.
Maxim is a horse
All horses are animals
All animals will die
therefore. Maxim will die
이처럼, 주어진 3개의 명제로부터, 새로운 1개의 명제를 증명하였다. 이같은 과정을 추론이라고 한다. 이를 predicate calculus로 나타내면 아래와 같다.
horse(Maxim)
∀X (horse(X) ⇒ animal(X))
∀Y (animal(Y) ⇒ die(Y))
therefore. horse(Maxim) ⇒ die(Maxim)
이를 다시 표현하면,
horse(Maxim)
-horse(X) ∨ animal(X)
-animal(Y) ∨ die(Y)
이다. 이것을 Resolution 에 의해 정리하면 아래표와 같게 된다.
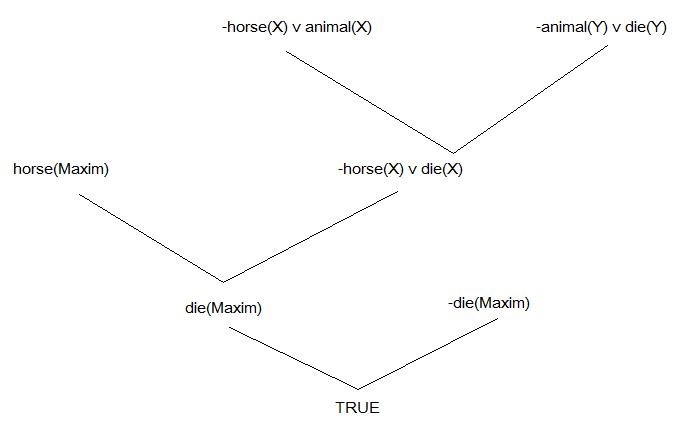
Figure 1. Resolution
추론 규칙은 sound 와 complete 의 2가지로 평가된다. 우선 sound는, 생성된 문장이 논리적으로 합당한 경우, 사용된 추론 규칙을 sound(정당) 하다고 한다. 예를들면, P와 P⇒Q 가 domain I 의 범위내에서 둘다 true일 때, 'modus ponens' 추론 규칙은 Q또한, true라는것을 알 수 있게 해준다 그리고 complete(완전) 은, 존재하는 모든 문장들이 추론규칙에 의해 논리적으로 합당하게 생성 될 수 있는 경우 추론규칙을 complete(완전) 하다고 한다. 아래는 사용 할 수 있는 추론 규칙에 대한 것이다.
- modus ponens : 만약 sentence P와 P ⇒ Q 가 참이라면, modus ponens 은 우리에게 Q가 참임을 암시한다.(추론한다.)
- modus tollens : 만약 P ⇒ Q가 참이고, Q가 거짓 이라면, 우리는 P가 거짓 이라는 걸 알 수 있다.
- and elimination : P ∧ Q가 참이면, P와 Q둘다 참이라는 것을 알 수 있다.
- and introduction : P와 Q가 참이면, P ∧ Q 가 참이라는 것을 알 수 있다.
- universal instantitation : p(X)로 표현된 식은, X의 도메인에 포함된 a로 치환한 p(a)로 표현할 수 있다.
'Courses > `2012 AI' 카테고리의 다른 글
| Predicate, Clause form 실습 (0) | 2012.05.07 |
|---|---|
| LISP (0) | 2012.05.01 |
| Resolution Theorem Proving (0) | 2012.05.01 |
| Unification (0) | 2012.05.01 |
| Calculus Introduction (0) | 2012.05.01 |